Allgemeine Wurzelfunktionen
Funktionen mit Gleichungen der Form
heißen Wurzelfunktionen.
Wurzelfunktionen sind spezielle Potenzfunktionen, wenn man als Exponenten nicht nur ganze Zahlen, sondern auch gebrochene Zahlen zulässt:
Als Wurzelfunktionen bezeichnet man im weiteren Sinne ebenfalls alle Funktionen, in deren Funktionsterm das Argument x als Bestandteil eines Wurzelradikanden auftritt, z. B. also:
Funktionen mit Gleichungen der Form
heißen Wurzelfunktionen.
Wurzelfunktionen sind spezielle Potenzfunktionen, wenn man als Exponenten nicht nur ganze Zahlen, sondern auch gebrochene Zahlen zulässt:
Anmerkung: Verwendet man die Bruchpotenzschreibweise, so muss gefordert werden, dass Bruchpotenzen nur für positive Basen erklärt sind.
Als Wurzelfunktionen bezeichnet man im weiteren Sinne ebenfalls alle Funktionen, in deren Funktionsterm das Argument x als Bestandteil eines Wurzelradikanden auftritt,
z. B. also .
Besonders häufig treten Funktionen mit Gleichungen der Form auf. Die Funktion ist die Umkehrfunktion (inverse Funktion) zu , jedoch nur für , da die Gleichung keine umkehrbar eindeutige (eineindeutige) Zuordnung beschreibt.
-
a ist die n-te Wurzel aus c
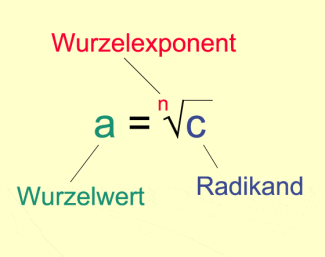
Anmerkung:
ist nicht äquivalent zu , da Quadrieren keine äquivalente Umformung darstellt. Zieht man auf beiden Seiten die Wurzel, dann erhält man nach der Quadratwurzeldefinition mit folgender Fallunterscheidung:
(1) , wenn
(2) , wenn
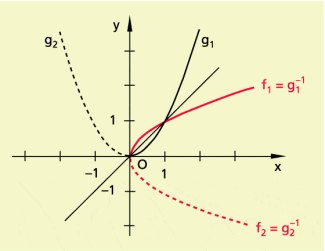
ist die Umkehrung von mit ,
ist die Umkehrung von mit (Bild 2).
-
Umkehrung der quadratischen Funktion
Für Wurzelfunktionen
gelten die Eigenschaften aus der Tabelle (Bild 3).
-
Eigenschaften der Wurzelfunktion


