Quadratische Gleichungen, Lösungsformel

Die Gleichung zur Berechnung der beiden Lösungen $x_{1} und x_{2}$ der quadratischen Gleichung aus den Parametern p und q heißt Lösungsformel einer quadratischen Gleichung in der Normalform.
Der Term ${(\frac{p}{2})}^{2} - q$ heißt Diskriminante der quadratischen Gleichung.

Allgemeine quadratische Gleichungen

#Einsetzungsverfahren #Ergänzungsverfahren #Lösungsverfahren #Quadratische Gleichung #Wurzelziehen #Ausklammern

Die Gleichung zur Berechnung der beiden Lösungen $x_{1} und x_{2}$ der quadratischen Gleichung aus den Parametern p und q heißt Lösungsformel einer quadratischen Gleichung in der Normalform.
Der Term ${(\frac{p}{2})}^{2} - q$ heißt Diskriminante der quadratischen
Gleichung.

Die Lösungsverfahren für quadratische Gleichungen wie Quadrieren, Wurzelziehen, Faktorisieren, Verwenden binomischer Formeln und quadratische Ergänzung führen nicht bei jeder quadratischen Gleichung der Form $y = x^{2} + p x + q$
zur Lösung.
Deshalb ist es zweckmäßig, die Umformungen allgemein mit beliebigen Parametern durchzuführen. Dadurch erhält man eine Formel, mit der die Lösungen direkt aus den Parametern berechnet werden können.

Herleitung der Lösungsformel für quadratische Gleichungen in der Normalform

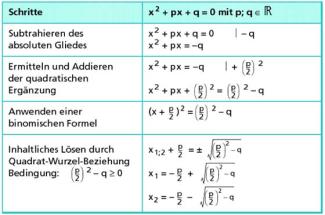
Als Ausgangsgleichung wird die Normalform einer quadratischen Gleichung mit den Parametern p und q gewählt. Bei der Herleitung der Lösungsformel werden sowohl die quadratische Ergänzung als auch die binomischen Formeln genutzt (Bild 1).
Die quadratische Gleichung $x^{2} + p x + q = 0$ mit den Parametern $p, q \in ℝ$ hat die Lösungen
$x_{1; 2} = - \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q} und der Bedingung {(\frac{p}{2})}^{2} - q \geq 0$
Ist ${(\frac{p}{2})}^{2} - q = 0$ hat die Gleichung die Doppellösung $x_{1} = x_{2} = - \frac{p}{2}$ .
Für ${(\frac{p}{2})}^{2} - q < 0$ hat die Gleichung keine reellen Lösungen.

Material zum Thema

BWS-MAT1-0418-03.mcd

BWS-MAT1-0418-03.mcd

Um eine quadratische Gleichung mithilfe der Lösungsformel zu lösen, sind die in Bild 2 dargestellten Schritte zu absolvieren.

Hinweise zum Lösen einer quadratischen Gleichung:

Versuche jede Gleichung zuerst inhaltlich zu lösen. Zum Beispiel:
- durch Wurzelziehen
- durch Umformen in eine Gleichung der Form
  $T_{1} \cdot T_{2} = 0$
- durch direkte Anwendung einer binomischen Formel.
Wenn du keine Möglichkeiten für eine inhaltliche Lösung siehst, forme die Gleichung in die Normalform um und löse sie mit der Lösungsformel.
Beachte stets, dass eine quadratische Gleichung keine, eine oder zwei Lösungen haben kann.

Schrittfolge beim Lösen einer quadratischen Gleichung mithilfe der Lösungsformel

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Quadratische Gleichungen, Lösungsformel

Allgemeine quadratische Gleichungen

BWS-MAT1-0418-03.mcd

Rechtliches

Einloggen