Arten mechanischer Arbeit

Mechanische Arbeit wird verrichtet, wenn ein Körper oder ein System durch eine einwirkende Kraft bewegt oder verformt wird. Dabei unterscheidet man traditionsgemäß je nach dem betreffenden Vorgang zwischen verschiedenen Arten der Arbeit. Wichtige Arten sind

	die Arbeit beim Heben eines Körpers (Hubarbeit),
	die Arbeit beim Beschleunigen eines Körpers (Beschleunigungsarbeit),
	die Arbeit beim Wirken von Reibungskräften (Reibungsarbeit),
	die Arbeit beim Dehnen einer Feder (Federspannarbeit) und
	die Arbeit beim Komprimieren eines Gases (Volumenarbeit).

Häufig wirken bei einem Vorgang auch mehrere Arten von Arbeit.

Arbeit in der Mechanik

#Arbeit #Energie #Hubarbeit #Spannarbeit #Lageenergie #Drehmoment

Umwandlung mechanischer Energie

#Arbeit #Energie #Hubarbeit #Spannarbeit #Lageenergie #Drehmoment

Häufig wirken bei einem Vorgang auch mehrere Arten von Arbeit. Das ist z.B. bei einem an einem Berg anfahrenden Auto der Fall: Es wird Beschleunigungsarbeit verrichtet, zugleich aber auch Reibungsarbeit und Hubarbeit (Bild 1).

Nachfolgend sind die einzelnen Arten mechanischer Arbeit genauer charakterisiert. Ein Überblick über die physikalische Größe mechanische Arbeit ist in einem weiteren Beitrag gegeben.

Hubarbeit

Die Hubarbeit ist eine Art der mechanischen Arbeit und wie jede Arbeit eine Prozessgröße. Hubarbeit wird z. B. verrichtet, wenn durch eine Kraft ein Körper gehoben wird, wenn man einen Koffer anhebt oder wenn man eine Treppe hinaufsteigt.
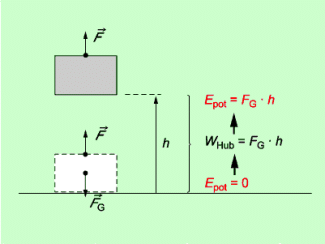
Die zum Heben eines Körpers erforderliche Kraft ist seine Gewichtskraft. Der beim Heben zurückgelegte Weg ist die Höhe, um die der Körper gehoben wird. Gewichtskraft und Weg habe die gleiche Richtung. Demzufolge kann die Hubarbeit berechnet werden mit der Gleichung:

$\begin{array}{l} W_{H} = F_{G} \cdot h oder \\ W_{H} = m \cdot g \cdot h \\ F_{G} Gewichtskraft des Körpers \\ h Höhe, um die der Körper \\ gehoben wird (Weg) \\ m Masse des Körpers \\ g Fallbeschleunigung (Ortsfaktor) \end{array}$

Beim Verrichten von Hubarbeit an einem Körper vergrößert sich dessen potenzielle Energie (Bild 2). Für den Zusammenhang zwischen der Hubarbeit und der Änderung der potenziellen Energie gilt:

$W_{H} = Δ E_{p o t}$

Beschleunigungsarbeit

Die Beschleunigungsarbeit ist eine Art der mechanischen Arbeit und wie jede Arbeit eine Prozessgröße. Beschleunigungsarbeit wird z. B. verrichtet, wenn ein Auto aus dem Stillstand in Bewegung gesetzt wird oder wenn eine Rakete startet (Bild 3).
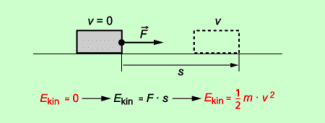
Allgemein gilt: Beschleunigungsarbeit wird verrichtet, wenn ein Körper durch eine Kraft beschleunigt wird. Ist diese Kraft konstant und wirkt sie in Richtung des Weges, so kann die Beschleunigungsarbeit berechnet werden mit der Gleichung:

$\begin{array}{l} W_{B} = F \cdot s \\ F beschleunigende Kraft \\ s zurückgelegter Weg \end{array}$

Ersetzt man die Kraft F durch das Produkt aus der Masse m des Körpers und der Beschleunigung a (newtonsches Grundgesetz), so erhält man als Gleichung zur Berechnung:

$\begin{array}{l} W_{B} = m \cdot a \cdot s \\ m Masse des Körpers \\ a Beschleunigung des Körpers \\ s zurückgelegter Weg \end{array}$

Beim Verrichten von Beschleunigungsarbeit an einem Körper vergrößert sich dessen kinetsche Energie (Bild 4). Für den Zusammenhang zwischen der Beschleunigungsarbeit und der Änderung der kinetischen Energie gilt:

$W_{B} = Δ E_{k i n}$

Reibungsarbeit

Die Reibungsarbeit ist eine Art der mechanischen Arbeit und wie jede Arbeit eine Prozessgröße. Reibungsarbeit wird z. B. verrichtet, wenn man mit dem Fahrrad rollt, auf Skiern einen Hang hinabgleitet (Bild 1) oder ein Auto abgebremst wird.
Die dabei wirkende bewegungshemmende Kraft ist die Reibungskraft. Der zurückgelegte Weg ergibt sich aus der Schnelligkeit der Bewegung des Körpers. Reibungskraft und Weg sind entgegengesetzt gerichtet. Ist die Reibungskraft konstant, so kann die Reibungsarbeit berechnet werden mit den Gleichungen:

$\begin{array}{l} W_{R} = F_{R} \cdot s \\ W_{R} = μ \cdot F_{N} \cdot s \\ F_{R} Reibungskraft \\ s zurückgelegter Weg \\ μ Reibungszahl \\ F_{N} Normalkraft (senkrecht auf die Unterlage \\ wirkende Kraft) \end{array}$

Beim Verrichten von Reibungsarbeit wird mechanische Energie in thermische Energie umgewandelt und in Form von Wärme an die Umgebung abgegeben. Für den Zusammenhang zwischen der Reibungsarbeit und der Änderung der mechanischen Energie gilt:

$W_{R} = Δ E_{m e c h}$

Auch beim gleichförmigen Fahren oder beim Beschleunigen eines Fahrzeuges wird Reibungsarbeit verrichtet. Beim gleichförmigen Fahren muss so viel Energie zugeführt werden, wie Reibungsarbeit verrichtet wird. Beim Beschleunigen ist die zugeführte Energie größer als die durch Reibung in Wärme umgewandelte Energie. In diesem Falle wird neben der Reibungsarbeit auch Beschleunigungsarbeit verrichtet.

Federspannarbeit

Die Verformungsarbeit ist eine Art der mechanischen Arbeit und wie jede Arbeit eine Prozessgröße. Verformungsarbeit wird z. B. verrichtet, wenn man einen Ast biegt, eine Feder oder einen Impander verformt. Die Arbeit zum Verformen einer Feder wird auch als Federspannarbeit bezeichnet.
Die dabei wirkende Kraft ist gleich der Kraft, mit der der Körper aufgrund seines Aufbaus wirkt. Der zurückgelegte Weg ergibt sich aus der Stärke der Verformung.
Bei einer elastischen Feder ist der Weg gleich der Dehnung der Feder. Beim Dehnen einer Feder ist die erforderliche Kraft nicht konstant. Sie nimmt mit der Dehnung der Feder zu, wobei für den elastischen Bereich das hookesche Gesetz gilt:

$s ~ F$

Somit kann man nicht die Gleichung anwenden. Die Federspannarbeit lässt sich aber mit einer mittleren Kraft berechnen, die wegen der Gültigkeit des hookeschen Gesetzes gleich der halben Endkraft ist. Es gilt für die Federspannarbeit:

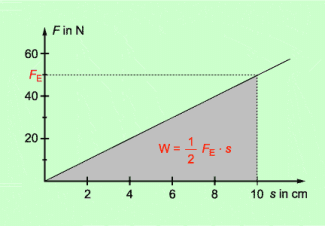
$\begin{array}{l} W_{F} = \frac{1}{2} F_{E} \cdot s \\ W_{F} = \frac{1}{2} D \cdot s^{2} \\ F_{E} Endkraft (Kraft bei der Ausdehnung s) \\ s Dehnung der Feder (Weg) \\ D Federkonstante \end{array}$

Stellt man die zum Dehnen einer Feder erforderliche Kraft in Abhängigkeit von der Dehnung der Feder dar, so erhält man eine Gerade (Bild 6): Die Dehnung der Feder ist der wirkenden Kraft proportional. Je größer die Dehnung der Feder ist, desto größer ist auch die erforderliche Kraft. Aus einem solchen F-s-Diagramm kann man auch die Federspannarbeit ermitteln: Die Federspannarbeit ist gleich der Fläche unter dem Graphen, wobei die auf den Achsen aufgetragenen Einheiten zu berücksichtigen sind. Man kann mithilfe dieses Verfahrens auch eine beliebige Verformungsarbeit bestimmen, wenn man den Verlauf des Graphen kennt. Auch bei einem beliebigen Kurvenverlauf des Graphen ist die Fläche unter ihm gleich der verrichteten mechanischen Arbeit.

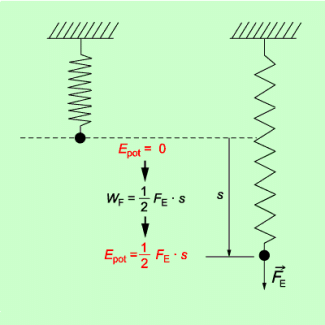
Beim Verrichten von Verformungsarbeit und speziell von Federspannarbeit vergrößert sich die in der Feder gespeicherte Energie. Es ist eine spezielle Form von potenzieller Energie. Allgemein gilt:
Die beim Dehnen einer Feder verrichtete Federspannarbeit ist genau so groß wie die dann in der Feder gespeicherte potenzielle Energie (Bild 7):

$W = F \cdot s$

Volumenarbeit

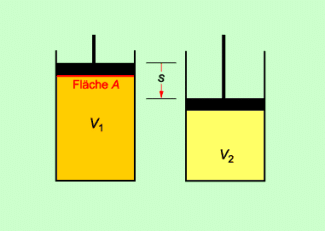
Die Volumenarbeit oder Volumenänderungsarbeit ist eine Art mechanischer Arbeitund wie jede Arbeit eine Prozessgröße. Volumenarbeit wird z. B. verrichtet, wenn man mit einer Luftpumpe Luft auf einen Reifen pumpt (Bild 8), der Kolben im Zylinder eines Verbrennungsmotors bewegt wird oder ein Luftballon aufgeblasen wird. Allgemein gilt:

Volumenänderungsarbeit wird verrichtet, wenn auf ein abgeschlossenes Gas eine Kraft wirkt und sich dabei das Volumen das Gases ändert.

Die Kraft kann dabei von außen über einen Kolben auf das Gas einwirken, wie das z. B. bei einer Luftpumpe der Fall ist.
Es können aber auch innere Kräfte wirken, wie z. B. im Zylinder eines Verbrennungsmotors: Durch Verbrennen von Benzin oder Dieselkraftstoff erhöht sich der Druck im Gas. Der Kolben wird dadurch bewegt und das Volumen des Gases vergrößert sich. Führt man einem abgeschlossenen Raum von außen Wärme zu, so vergrößert sich ebenfalls der Druck in dem abgeschlossenen Raum. Auch das kann zu einer Volumenänderung führen. Es wird Volumenänderungsarbeit verrichtet. Das ist z. B. bei einer Luftmatratze der Fall, die sich erst im Wasser befand und anschließend in die pralle Sonne gelegt wird.
Für einen speziellen Fall lässt sich die Volumenänderungsarbeit relativ einfach berechnen.

Unter der Bedingung, dass der Druck in dem Gas bei der Volumenänderung konstant ist, lässt sich die Volumenänderungsarbeit mit folgender Gleichung berechnen:

$\begin{array}{l} W_{A} = p \cdot Δ V \\ p Druck im Gas \\ Δ V Änderung des Gasvolumens \end{array}$

Die Volumenänderung ist gleich der Differenz zwischen dem Endvolumen und dem Anfangsvolumen. Vergrößert sich das Volumen, dann ist die Differenz positiv. Bei Volumenverkleinerung ist die Differenz negativ. Vereinbarungsgemäß wird nun aber in der Physik die an einem abgeschlossenen System verrichtet Arbeit (Volumenverkleinerung) mit einem positiven Vorzeichen und die von einem System verrichtete Arbeit (Volumenvergrößerung) mit einem negativen Vorzeichen versehen. Um beiden Festlegungen gerecht zu werden, schreibt man auch manchmal für die Volumenänderungsarbeit:

$W_{A} = - p \cdot Δ V$

Das Vorzeichen ergibt sich aus den obigen Festlegungen. Es beinhaltet eine Aussage darüber, ob an einem System (Volumenverkleinerung) oder von einem System (Volumenvergrößerung) Arbeit verrichtet wird.

Die genannte Gleichung kann man aus der allgemeinen Gleichung

$W = F \cdot s$ (1)

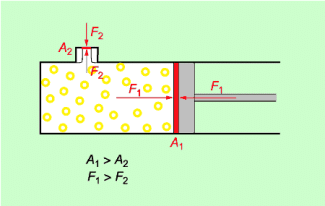
zur Berechnung der mechanischen Arbeit herleiten. Wir betrachten dazu die Arbeit, die beim Hineinschieben eines Kolbens in einen Zylinder verrichtet wird (Bild 10).
Die konstante Kraft F ist gleich dem Produkt aus dem konstanten Druck p und der Fläche A des Kolbens:

$F = p \cdot A$ (2)

Der Weg kann aus der Volumenänderung und der Fläche des Kolbens berechnet werden:

$s = \frac{Δ V}{A}$ (3)

Setzt man die Gleichungen (2) und (3) in die rechte Seite der Gleichung (1) ein, so erhält man:

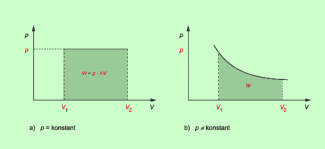
$\begin{array}{l} W = p \cdot A \cdot \frac{Δ V}{A} \\ W = p \cdot Δ V \end{array}$

Die Volumenänderungsarbeit kann auch als einem p-V-Diagramm (Druck-Volumen-Diagramm) ermittelt werden (Bild 11a). Die Volumenänderungsarbeit ist gleich der Fläche unter dem Graphen, wobei für eine Angabe des Wertes die auf den Achsen abgetragenen Einheiten zu beachten sind. Die Bestimmung der Volumenänderungsarbeit ist aus einem Diagramm auch dann möglich, wenn der Druck nicht konstant ist (Bild 11b). Dann kann man die Arbeit durch Auszählen der Fläche ermitteln.
Die Volumenänderungsarbeit spielt vor allem bei Verbrennungsmotoren (Dieselmotoren, Ottomotoren) sowie bei Dampfmaschinen eine entscheidende Rolle. Dabei wird vom Gas mechanische Arbeit verrichtet. Sie wird genutzt, um Fahrzeuge und Maschinen anzutreiben.

Ist der Druck nicht konstant, so kann die Volumenarbeit in einem beliebigen Fall berechnet werden mit der Gleichung:

$W = \int_{V_{1}}^{V_{2}} p (V) d V$

Voraussetzung für die Berechnung ist, dass man die Funktion p = p(V) kennt oder sich herleiten kann. Ist das nicht der Fall, dann kann die Arbeit nur durch Auszählen der Fläche unter dem Graphen im p-V-Diagramm ermittelt werden.