Wurzelgleichungen
Eine Gleichung heißt Wurzelgleichung, wenn die Variable im Radikanden auftritt.
Wenn es sich beim Lösen von Gleichungen um Quadratwurzeln handelt, ist es oftmals möglich, diese Wurzeln durch einmaliges oder mehrfaches Quadrieren zu beseitigen. Allerdings muss das Ergebnis unbedingt überprüft werden, da das Quadrieren keine äquivalente Umformung ist.
Eine Gleichung heißt Wurzelgleichung, wenn die Variable im Radikanden auftritt.
Wenn es sich beim Lösen von Gleichungen um Quadratwurzeln handelt, ist es oftmals möglich, diese Wurzeln durch einmaliges oder mehrfaches Quadrieren zu beseitigen. Allerdings muss das Ergebnis unbedingt überprüft werden, da das Quadrieren keine äquivalente Umformung ist.
Beispiele:
|
|
|
-
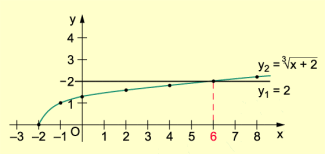
Grafische Lösung